The Perspective Model

In the previous post, I spoke about Shape from Shading – the idea and the concepts related to shape from shading, in particular orthographic shape from shading. Also I presented some of my results that were obtained for a synthetic test image. In this post, I would like to talk about another model for shape from shading – the Perspective Shape from Shading.

Before we start the discussion on the perspective projection model, let us discuss the problems associated with the orthographic model. In the orthographic model, we obtain an Eikonal type HJE, which reads as,

\[\begin{equation} | \nabla u | = \sqrt{\frac{1}{I(x)^2}-1}. \end{equation}\]

This PDE, coupled with an appropriate boundary condition, is an example of an ILL-POSED problem. That is, the PDE, does not have a unique solution at certain points. Physically, these points are the places where \(I(x) = 1\) or “Bright spots”. At these bright spots, the surface can have a minimum/maximum. Well, to overcome this, we must supply the information at these “Singularity points” to make the problem WELL-POSED. But we might not have this information with us all the time. We are now in need of a much more realistic model to describe the situation. This is where the perspective model comes in.

Orthographic view is just plain old projection of the object onto a plane, ignoring the effects of depth . Whereas the perspective projection, takes into account, the effect of depth. The classic example is a long corridor or a railway track. In these examples, the lines which are actually parallel, “appears” to converge to a point when we see it. This is called the perspective view. Incorporating this makes the model close to the real life scenario.

Naturally incorporating this makes the model complex. Naturally as the model becomes complex, our Hamilton Jacobi Equation gets more complex as well. For the perspective projection model our HJE becomes,

\[\begin{equation} -e^{-2v} + \frac{I(x)f^2}{Q(x)}\sqrt{f^2|\nabla v|^2 + (x.\nabla v)^2 + Q(x)^2} = 0, \end{equation}\]

where

\[\begin{equation} Q(x) = \sqrt{\frac{f^2}{|x|^2+f^2}}, \end{equation}\]

\(\nabla v\) denotes the gradient of \(v\) and \(f\), the focal length of the camera. To recover the surface, we solve for \(v\). To do this, we use numerical schemes to solve the HJ equations. Some interesting results are lined up below.

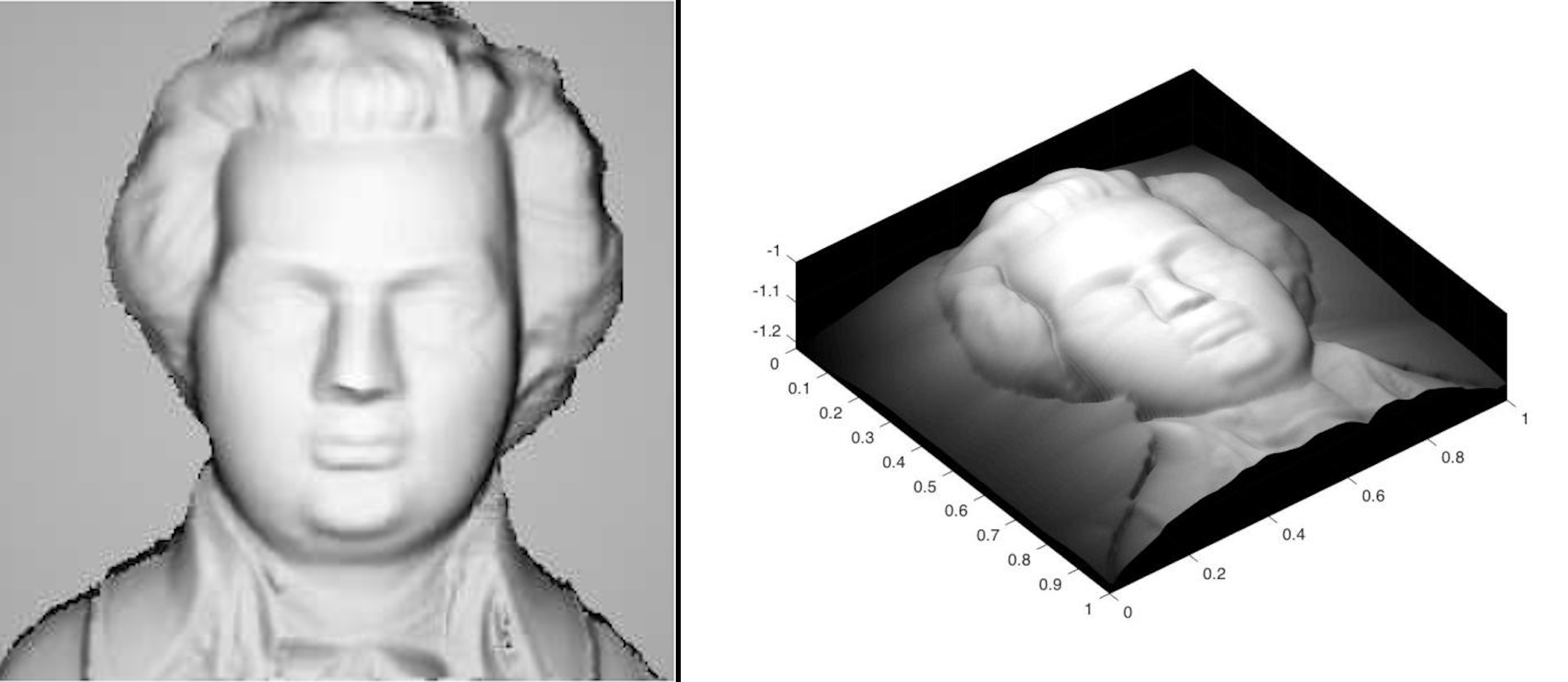
This model was developed by Prados and Faugeras, INRIA in their thesis titled “Shape from Shading – a well posed problem?” The images used for reconstruction here are the ones directly obtained from Prados’ and Faugeras’ technical report.