Postdoc at Umeå University, Sweden
Shape from Shading (SFS)
The idea of SFS is to reconstruct an object (Shape) from a 2D Image (Shading). There are a lot of ways to reconstruct a 3D Object from a 2D Image. Similar methods include Shape from Stereo, Shape from Contours, Shape from Silhouettes etc.
In this short blog post, I should be able to summarize the nature of the problem, its PDE and some issues. Here we go!
Brightness Equation
Imagine a surface on which light is being shined on. Let the direction of the unit light vector be \(\vec{L}\) . Also assume that the unit normal on the surface is \(\vec{n}\) . According to the Lambert’s Cosine Law,
The radiant intensity \(R\) is directly proportional to the cosine of the angle between the Light Vector \(\vec{L}\) and the surface normal \(\vec{n}\). Also the intensity map (the input) I is assumed to be the reflectance map. This means we have the relation,
\[I(x) = R = cos(\theta) = \vec{L} . \vec{n}\]This equation is known as the brightness equation. Several mathematical models have been developed using this Equation. Some of them include the models proposed by Rouy and Tourin, Prados and Faugeras etc.
Explanation
Now that the derivation of the equation is done, let me explain what it exactly is.
Consider this diagram of a dome with the green arrows indicating the light vector and the purple ones indicating the direction of the unit normal.
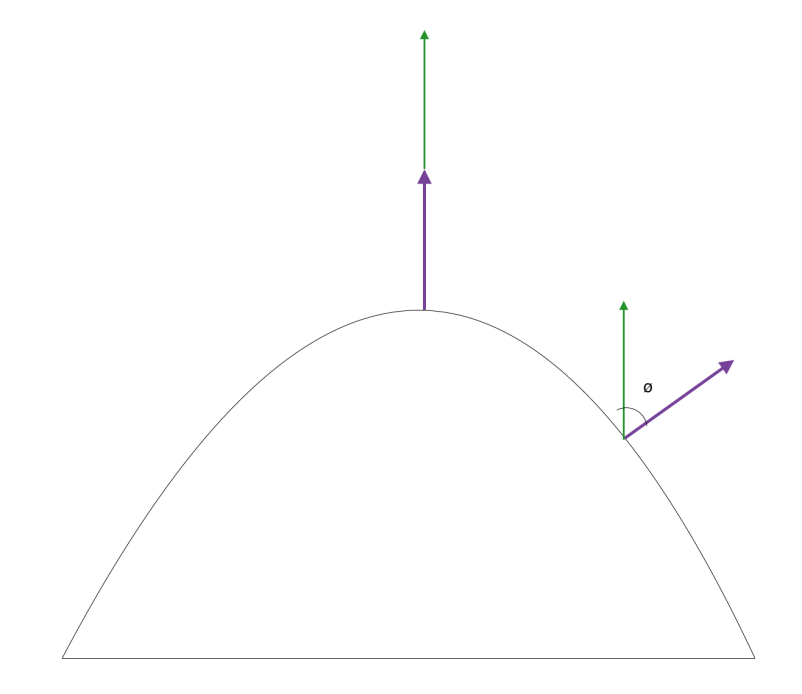
If the unit normal is along the light direction, we see that we get the maximum intensity \(\cos(0) = 1\). This means we may have the peak of a dome. If the unit normal is aligned at an angle \(\phi\) , then we have a some point where the intensity is between \(0\) and \(1\) and if \(\phi = \frac{\pi}{2}\) , then the intensity is zero.
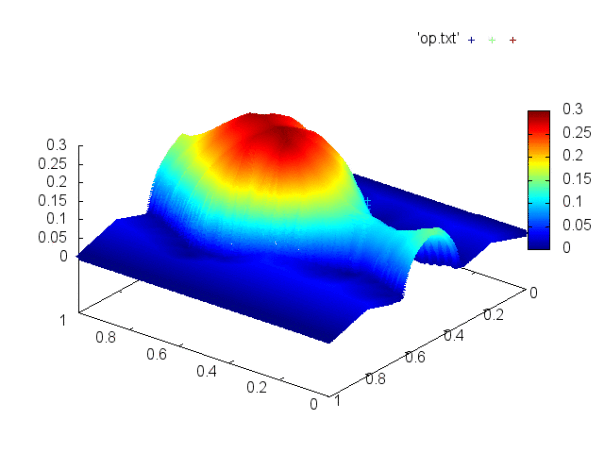
So, we might want to consider giving an image like this one, for example, to get the 3D Shape of a dome.

Some Math
The PDE that describes the above problem formulation is of the Eikonal type, i.e.,
\[|\nabla u | = \sqrt{\frac{1}{I(x)^2}-1}.\]Some issues of this PDE is that we cannot find a smooth function that solves it. We must make an attempt to find “weaker” solutions to this PDE known as Viscosity solutions. It is weak in the sense that, it satisfies the PDE, but may not be differentiable everywhere. So a rigorous mathematical framework is necessary to find the solutions to it.
Issues
Some of you must have guessed the weakness in this type of approach. On taking a close look at the second image in this article, we notice that, the same image can be obtained from a dome or a bowl. The intensity may be unity at peaks as well as troughs. So we have a problem of non-uniqueness. So, to solve this problem, explicit information must be given at places where the intensity is unity – whether it is a dome (positive height) or a bowl (negative height).
This can be seen from the PDE as when \(I(x) = 1\), the equation becomes
\[|\nabla u | = 0.\]By the theory of viscosity solutions, the viscosity sub-solution condition is violated in this case, which is very much essential to guarantee the uniqueness of solution.
To overcome this, we need to specify information at the bright spots. This cannot be possible always as we might not know about the nature of the object before attempting to actually reconstruct it.
EDIT: My results
So 2 days ago I published this blog post which illustrates the concept of Shape from Shading. I tried out the SFS Models proposed by Rouy and Tourin, Prados and Faugeras and the results came out pretty neat!
I consider the following “Test Vase” for reconstruction.

The image is read using MATLAB, converted to a normalized gray scale image and written in a text file using
dlmwrite('filename',M)
where \(M\) is an array.
The text file now contains the Matrix, that describes the image intensity and is read by a Fortran90 Code. The PDE is then solved using a Finite Volume Scheme.
Orthographic Model – Rouy and Tourin